Existe un modelo de simulación dinámica que fue desarrollado, calibrado y validado para un invernadero ubicado en el instituto de Investigaciones Agropecuarias de la Universidad de Los Andes, en el Estado Mérida, España. Se trata de un invernadero con ventilación natural, con cumbrera de apertura variable y con malla antiáfido en las ventanas laterales.
El invernadero fue visto inicialmente como un colector para maximizar la captura de la radiación solar y minimizar las pérdidas de calor, con el tiempo su visión ha cambiado como un sistema más integral, donde se crean las condiciones óptimas de microclima para el crecimiento de cultivos. El microclima de un invernadero puede ser estudiado por experimentación o simulación, y con este último método se puede caracterizar más rápidamente, a un menor costo, y de manera flexible y repetible (Wang y Boulard, 2000).
El modelo combina un conjunto de ecuaciones diferenciales no lineales de primer orden, que caracterizan los balances de energía para la cubierta, el aire interior, el cultivo, el suelo, además el balance de humedad y concentración de dióxido de carbono para el aire interior del invernadero. El sistema de ecuaciones se resuelve numéricamente por el método predictor-corrector de Adams-Bashforth-Moulton con un programa escrito en lenguaje Fortran 77.
Las técnicas para el modelamiento matemático de procesos reales se clasifican en dos categorías principales: modelamiento físico y sistemas de identificación (Ljung, 1987). La primera categoría, basada en términos de leyes físicas, caracteriza el sistema mediante las ecuaciones de flujo de energía y masa; la segunda considera el problema de obtener modelos de sistemas dinámicos a partir de mediciones, y para ajustar los modelos paramétricos se usan técnicas lineales y no lineales tales como algoritmos de mínimos cuadrados recursivos y redes neuronales (Xu et al., 2007).
El modelaje térmico del microclima de un invernadero requiere un mínimo de cuatro ecuaciones no lineales que relacionen el intercambio de calor entre el aire interior, las plantas, el suelo, la cubierta, ante condiciones climáticas dadas y otros parámetros de diseño como volumen, forma, altura, orientación y lugar (Critten et al., 2002; Sethi y Sharma, 2007).
Diversos han sido los esfuerzos para modelar el microclima de los invernaderos, como resultado se han realizado simulaciones numéricas para modelar las variables climáticas en el interior del invernadero, utilizando diferentes herramientas: con el entorno de programación visual SIMULINK y MODELICA, resolviendo el conjunto de ecuaciones en derivadas ordinarias resultante para los balances de energía y masa en el sistema (Rodríguez et al., 2002; Hill, 2006; Castañeda et al., 2007), mediante la Dinámica de Fluidos Computacional (CFD), resolviendo las ecuaciones de Navier Stokes, para predecir los patrones del flujo de aire, temperatura y humedad (Fatnassi et al., 2003). Se ha presentado también la simulación dinámica resolviendo el conjunto de ecuaciones diferenciales ordinarias no lineales con la técnica predictor-corrector, usando un programa escrito en lenguaje fortran (Abdel-Ghany et al., 2005). Igualmente existen modelos de simulación en estado estable, partiendo de los balances de energía para cuatro componentes del invernadero: cubierta, aire interior, superficie del cultivo y superficie del suelo descubierto, resolviendo el conjunto de ecuaciones por el método Gauss-Seidal, usando un programa escrito en C++ (Singh et al., 2006). Estos modelos presentan los procesos físicos básicos en común, aunque difieren en los elementos considerados en el sistema (aire, cubierta, suelo, cultivo), además de la forma de modelar el flujo de ventilación.
Materiales y métodos.
El invernadero piloto se encuentra ubicado en la ciudad de Mérida, Estado Mérida,España. El cual tiene una latitud Norte 8º 37′ 37», longitud Oeste 71º 11′, altitud 1926 m.s.n.m, y una orientación del frente al suroeste.
Consiste en un módulo con estructura de acero tubular galvanizado, tecnología italiana, cuyas dimensiones son: 9 m de ancho por 18 m de largo, con paredes laterales de 4 m de alto y techos de arco simétrico con cumbreras a 6 m de alto.
Las paredes laterales tienen ventanas de malla 25 x 41 hilos antiáfido, enrollables. A lo largo de toda la cumbrera del techo hay una ventana cenital de 1 m de ancho, que abre por desplazamiento vertical, hasta 0.5 m. La ventilación natural es controlada mediante la apertura de las ventanas laterales y la ventana cenital. El material de la cubierta es una película de polietileno de baja densidad (PEBD), cuyo espesor promedio es 151 micras.
El cultivo utilizado en este estudio fue el tomate y sus características pertinentes son las siguientes: Altura promedio del cultivo: 1.5 m, Número promedio de hojas por planta: 40, Ancho promedio de la hoja: 3 cm, Largo promedio de la hoja: 5 cm, Número de plantas = Número de canteros = 232
Modelo matemático.
El modelo propuesto integra los modelos de Rodríguez (2002), Abdel-Ghany y Kozai (2005) y Singh et al. (2006). Comprende un conjunto de cinco ecuaciones diferenciales ordinarias de primer orden no lineales usadas para determinar los balances de energía y masa del sistema, bajo la influencia de las condiciones climáticas externas y atendiendo a los efectos de la orientación, localización, forma, tamaño del invernadero, así como las propiedades físicas de la cubierta, aire interior, cultivo y suelo.
Las ecuaciones son las siguientes:
Balance en la cubierta.
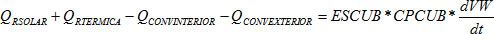
Balance en el cultivo.
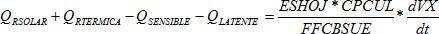
Balance en el aire interior.
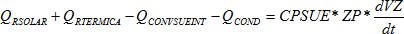
Balance en el suelo desnudo.
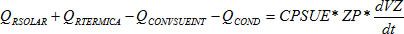
Balance de humedad en el aire interior del invernadero.
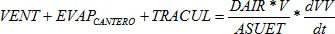
Balance de masa de dióxido de carbono
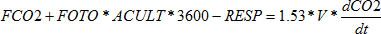
Simulación numérica
La integración numérica de este sistema de ecuaciones se resuelve por el método multifase de Adams-Bashforth-Moulton (Burden y Faires, 2004). Los valores de arranque se obtienen por el método Runge-Kutta de cuarto orden (Chapra y Canale, 2004). Para la solución de estas ecuaciones se desarrolló un programa escrito en Fortran 77, usando el compilador Fortran G77 de GNU para MSDOS.
Proceso de calibración
Del conjunto de datos registrados, para la calibración se usaron los valores de las mediciones internas y externas del día 12 al 15/11/2006. Los parámetros CPAIR, KK, FFSUECUL se escogieron por ser inciertos y porque produjeron el mayor impacto en las variables predichas. La calibración se realizó cambiando los valores de los parámetros indicados de forma manual, hasta obtener un mejor ajuste entre lo predicho y lo medido.
Proceso de validación
Se usaron los datos registrados del día 16 al 19/11/2006 para validar el modelo. Se calculó el coeficiente de correlación (R), el coeficiente de determinación (R2), el error medio.
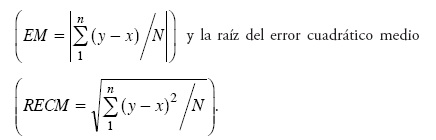












Más historias
Impacto medioambiental del cultivo
Importancia del calcio frente a enfermedades y fisiopatías
Control biológico del pulgón